In search of randomness: pseudo-random, algorithms and nature
To me, drawing happens in two steps. First, I think of a shape or a line to draw. Then, I decide where this shape or line should exist on a surface. When drawing pen on paper, this is pretty intuitive. In generative art, not so much. For the purpose of this article, lets assume step 1 is fairly easy. Step 2, on the other hand is much more complex. If I give instruction to draw a shape at one position, then a composition wouldn't be generative, it would be static. In generative art, the computer needs to assume and guess where you'd like to draw your shapes, and we need to help it. So far, my explorations led me from pseudo-randomness to nature, which I think mark both ends of a randomness spectrum when applied to the generative art domain. This article isn't a complete list, but just a few of my observations so far on how we can better understand and use randomness in generative art.
Just random
In Javascript, we have a neat math function able to give a number between 0 and 1. This is super handy, but leads to underwhelming results at larger scales. When using this math function to generate multiple values, each of those values is unaware of other values. This can explain why a set of random values can often be poorly distributed in a given range. In 2D space (on a canvas), this can lead to unattractive, or unbalanced compositions.
The best use of noisy (explain noisy) randomness is in places where the value becomes mostly invisible. Either because it has little impact or variation on the output, or because it is layered with many other random values.
Algorithms
Just using noisy randomness can get you far, especially when starting out with generative art. After a point, the use of noisy randomness becomes some kind of habit, or pattern. In my work, I started questioning noisy randomness. I found answers in mathematics, inspired by the work of Daniel Shiffman. Far from being a math person, I knew that much smarter people had already asked, and answered, similar problems.
Most often, algorithms are created to simulate and explain natural phenomena. The cool side effect is that they are fascinating to look at.
-
Voronoi tessellation can help understand proximity, and how people choose to travel to the closest available thing, given the option
-
The space colonization algorithm creates a network of paths that efficiently visit a set of points in space.
-
The meander network formation algorithm can move methodically through a set of points using a single line.
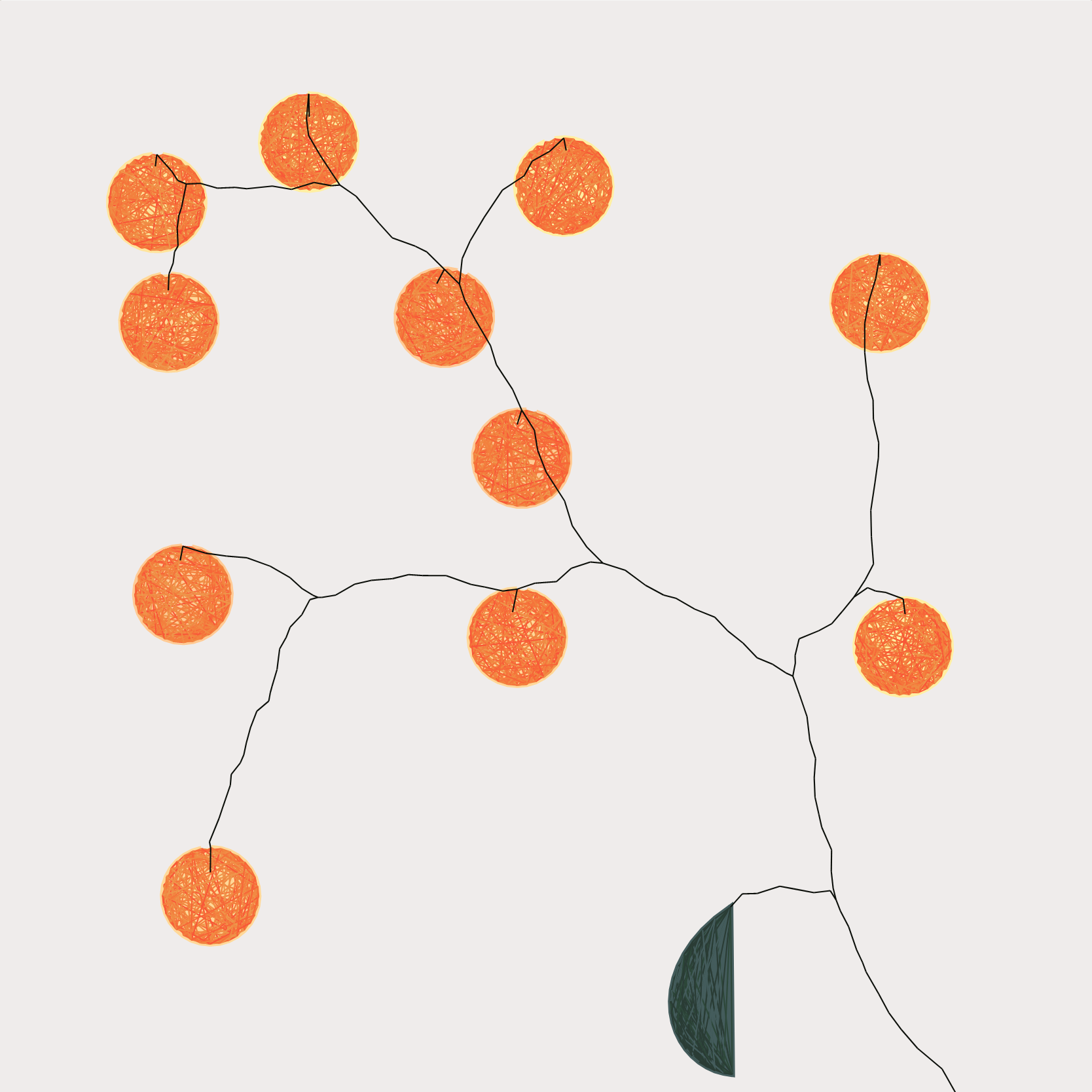
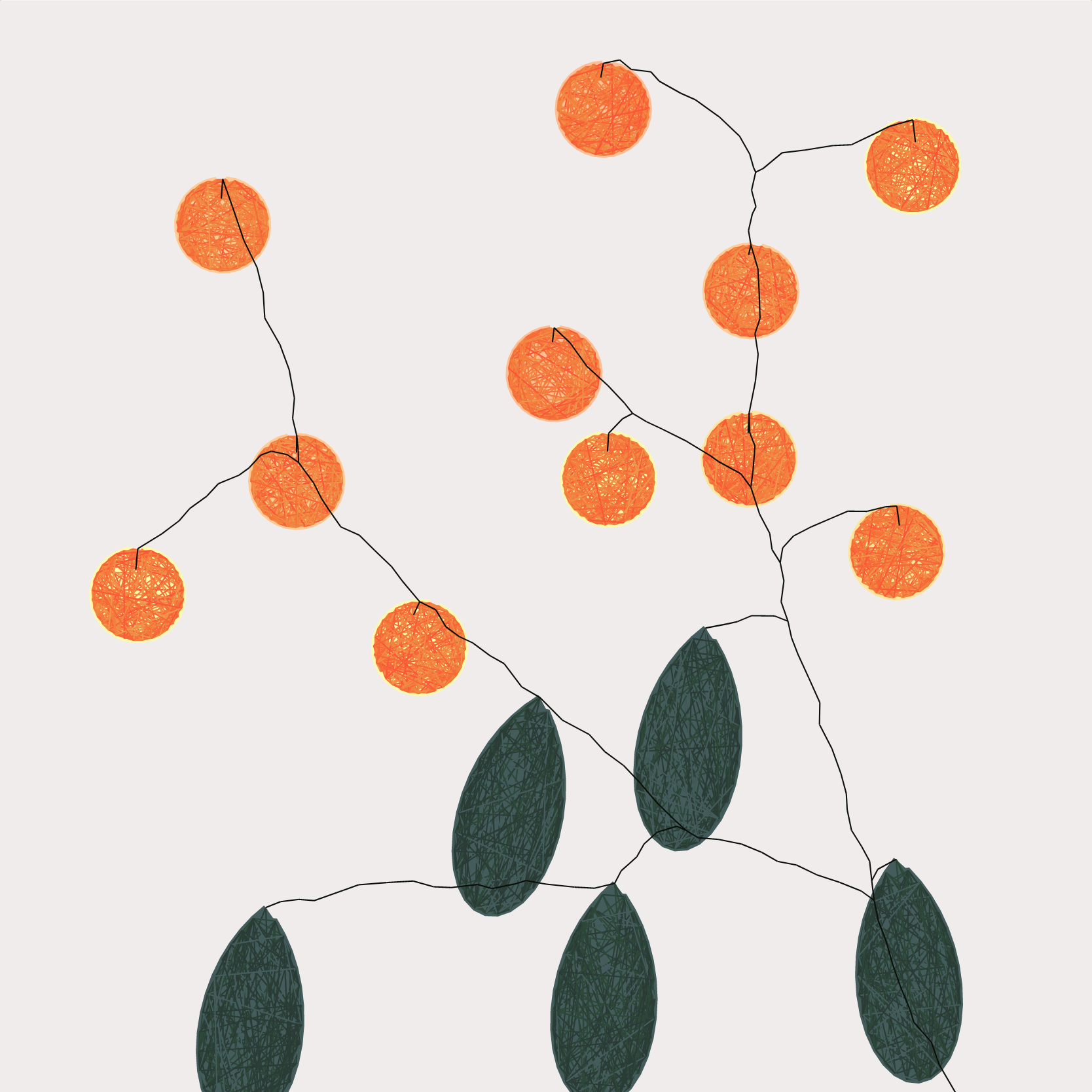 Both Voronoi tesselation and the space colonization algorithms create plant like compositions. Even then, all compositions are very similar to each other.Generate a Space Colonization
Both Voronoi tesselation and the space colonization algorithms create plant like compositions. Even then, all compositions are very similar to each other.Generate a Space Colonization
 Halton Sequence is slightly unpredictable, it can both look organic and ordered.Generate a Halton sequence
Halton Sequence is slightly unpredictable, it can both look organic and ordered.Generate a Halton sequence
Nature
By far the most complex form of randomness is simply present around us. You can appreciate randomness by looking or listening at nature. Listen to the birds song, look at the clouds in the sky, observe the grain pattern of a rock, listen to a crowd of people talking. In isolation, all of these are fascinating examples of randomness.
Now imagine layering these examples and creating a composite randomness, truly unpredictable, with great variation. A sky could be cloudy, but it could also be clear. Even while cloudy, the type and density of clouds will have a big impact on how it looks like. You will find similitudes, but never the same cloud. At least, you won't remember it.
If we hook up a machine to sense these inputs, like a camera or a microphone, we can turn nature into parameters for generative art. These parameters can help generate randomness in generative art by providing data that can be transposed into something else. I first encountered this technique from David Bowen's Cloud Piano installation. This installation looks at the clouds, or the sky, and transposes the current clouds into notes played on a piano.
Finding a data source becomes the main challenge of this type of generative artwork. At the simplest, it involves sensing the environment, just like humans sense the environment. Through, vision, hearing, or smelling, data can be captured from the world and used as random data. The artwork may have nothing to do with the origin of the data, and perhaps nothing to do with the input modality. In the cloud piano example, vision is used to generate sound.
To me, the transposition is where nature and generative art becomes really interesting. How we articulate the relation between input and output provides the meaning layer for an artwork.
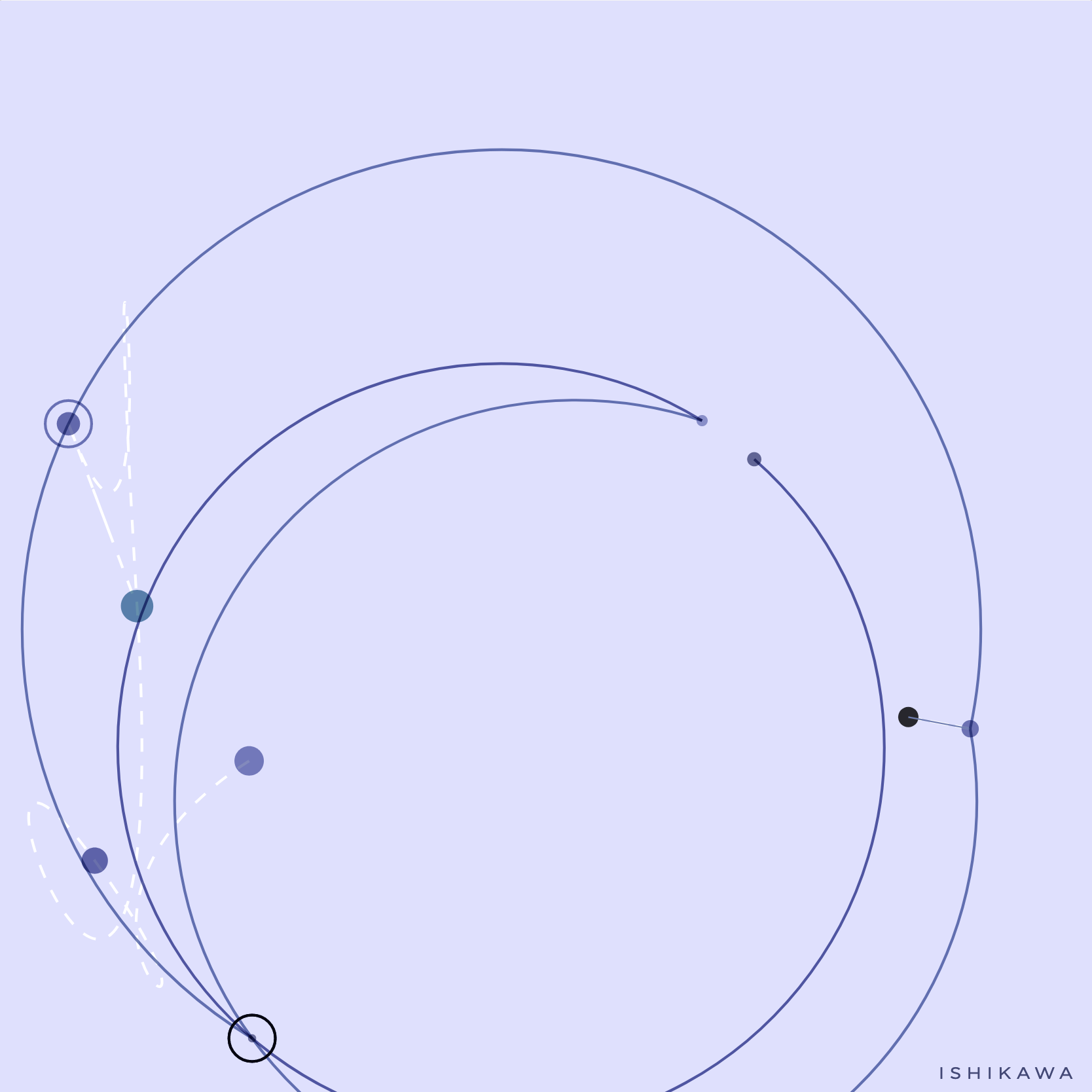

Everything together. Chaos?
Above, I've hinted at a layering technique, to reduce or improve the visibility of any type of algorithm. For noise, it is easy to use in less meaningful areas because it is cheap to use. Algorithms can be efficient, but they can also not be. A inefficient algorithm will have an impact on the time it takes to generate something. This might not be a deal breaker, but quick outputs are usually very satisfying. Some people don't mind slow generative artworks, and will use this as an opportunity to animate an output. So inefficient algorithms are definitely not a problem.
However, if speed is something that you require, I found that layering different types of randomness can lead to quick and satisfying disposable generative pieces. You can use one or two inefficient algorithms to generate a base set of data to interpret, and layer it in noise to add vibrancy and liveliness. Too much noise will ruin the natural beauty of the algorithm or data set you use, so it does require some fine tuning. And this is the joy of generative art: tweaking noise so that the output feels just right, most times.
Even more fine tuning.
After writing this first draft, generative artist Amy Goodchild published an article about distributing randomness. Amy uses the concept of skew to give depth to a set of random points. I think this goes in the same way of my explorations into different random point generation. Layering algorithms, nature and skew could lead to remarkable generative outputs.
